Zur Berechnung der Brechungswinkel sowie der Transmissions- und Reflexionskoeffizienten wurden das SNELL´sche Gesetz sowie die FRESNEL´schen Gleichungen benutzt. Zur Vereinfachung der Berechnungen wurde das Programm FRESNEL verwendet.

An Hand der nachfolgenden Skizze 1 sollen mögliche Strahlenverläufe diskutiert werden, die sich bei einer Einkopplung von Licht in den Objektträger ergeben können. Dargestellt ist der Querschnitt durch einen Objektträger. Alle Winkelangaben im nachfolgenden Text beziehen sich gemäß der physikalischen Definition auf den Winkel zwischen Lot und Strahl.



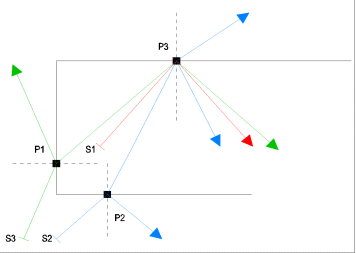
Fall 1: Einstrahlung über die Kante des Objektträgers (grüner Lichtstrahl S3):

S3 fällt auf die linke Kante des Objektträgers. Er wird im Punkt P1 teilweise reflektiert und teilweise gebrochen. Der Brechungswinkel kann theoretisch höchstens 41,8° betragen. Dieser Winkel stellt den Grenzwinkel der Totalreflexion dar, der sich bei umgekehrtem Strahlenverlauf von Glas nach Luft ergeben würde. Er kann nur erreicht werden, wenn der Einfallswinkel bei P1 nahezu 90° beträgt. In diesem Fall ergibt sich ein hoher Reflexionsanteil, sodass die Intensität des gebrochenen Strahls minimal wäre (siehe nachfolgende Tabelle 1 zur Abschätzung von Reflexion und Transmission). Der Strahl würde im Punkt P3 unter einem Winkel von 48,2° = 90° - 41,8° auf die Oberseite des Objektträgers fallen und an ihr total reflektiert. Kleinere Winkel als 48,2° sind bei P3 durch eine Beleuchtung über die Objektträgerkante auf keinen Fall zu erreichen. Insbesondere der Grenzwinkel der Totalreflexion von 41,8° (roter Strahl S1 in Skizze 1) kann nicht erreicht werden.
Entscheidend für die Beleuchtung der Oberfläche des Trägers ist der Transmissionskoeffizient t mit dem über die Kante bei P1 eingestrahlt werden kann. Bereits bei einem Einfallswinkel von a = 83° ergibt sich ein Transmissionskoeffizient von etwa t = 50% bei einem Brechungswinkel von b = 41,4° bei P1 und einem Reflexionswinkel von 48,6° an der Oberfläche des Objektträgers im Punkt P3. Da die Einstrahlung in die Kante des Objektträgers mit diffusem Licht erfolgt, kann davon ausgegangen werden, dass sich genügend Lichtstrahlen mit ausreichender Intensität einstellen werden, die durch Totalreflexion an Ober- und Unterfläche durch den Objektträger laufen. Kein Lichtstrahl, der über die Kante des Objektträgers eintritt kann aus der Oberseite des Trägers austreten und somit zu störenden Lichtreflexen führen. Dies stellt eine wesentliche Bedingung der hier beschriebenen Beleuchtungstechnik dar.

Tabelle zur Abschätzung von Reflexionskoeffizient r und Transmissionskoeffizient t in Abhängigkeit von Einfallswinkel a und Brechungswinkel b beim Übergang von Luft nach Glas

Fall 2: Einstrahlung über die Unterseite des Objektträgers (blauer Lichtstrahl S2)

Da der Objektträger in eine etwa 1mm tiefe Nut der Beleuchtungseinrichtung eingeschoben wird (siehe Kapitel 3.1) , ist in diesem Bereich auch eine Beleuchtung über die Unterseite möglich. Alle Strahlen S2 werden an Ober- und Unterseite des Objektträgers gebrochen und reflektiert. Keiner der Strahlen, die im Punkt P3 die Oberseite erreichen wird total reflektiert. Die Verluste durch Brechung in das Medium Luft führen zu einer schnellen Abnahme der Strahlintensität. Bereits bei einem Einfallwinkel von 40° im Punkt P3 treten 70% der Strahlintensität aus dem Objektträger aus. Nach vier Reflexionen an Ober- und Unterseite im Innern des Objektträgers ist die Intensität des eingetretenen Strahls auf weniger als 1% zurückgegangen. Dies bedeutet einerseits, dass eine Einstrahlung über die Unterseite des Objektträgers nicht zur angestrebten Beleuchtung beitragen kann. Andererseits können störende Auskopplungen des Lichts aus der Oberseite des Objektträgers nur im unmittelbaren Randbereich der Beleuchtungseinrichtung auftreten.


FAZIT aus 2.1: